LAS LÚNULAS DE HIPÓCRATES
Hipócrates de Chíos resolvió la cuadratura de las lúnulas y esto hizo pensar a los geómetras griegos que estaban en el camino de la cuadratura del círculo. Éste resultó ser uno de los tres problemas irresulubles con regla y compás.
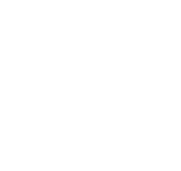
Sea un triángulo formado por el diámetro a de un círculo y dos cuerdas cualesquiera de éste, de longitud conocida (b y c). Sean dos semicírculos cuyos diámetros son las dos cuerdas b y c. Llamamos lúnulas a las regiones curvas que quedan dentro de estos semicírculos pero fuera del círculo de diámetro d. ¿Cuál es el área de las dos lúnulas formadas?
Conocimientos necesarios:
-
Teorema: El ángulo central de un círculo es el doble del ángulo inscrito en él y cuyo arco es el mismo.
-
Teorema de Pitágoras.
-
Operaciones con potencias y raíces.