Mathematika.org
by
Pablo Martín Bayón
is licensed under a
Creative Commons Attribution-ShareAlike 3.0 Unported License
PROBLEMAS CLÁSICOS |
 |
|
22-01-2025
AccederPROBLEMAS CLÁSICOS |
|
|
Mathematika.org
by
Pablo Martín Bayón
is licensed under a
Creative Commons Attribution-ShareAlike 3.0 Unported License
2020-03-17 12:56:41
Hipócrates de Chíos resolvió la cuadratura de las lúnulas y esto hizo pensar a los geómetras griegos que estaban en el camino de la cuadratura del círculo. Éste resultó ser uno de los tres problemas irresulubles con regla y compás.
Sea un triángulo formado por el diámetro a de un círculo y dos cuerdas cualesquiera de éste, de longitud conocida (b y c). Sean dos semicírculos cuyos diámetros son las dos cuerdas b y c. Llamamos lúnulas a las regiones curvas que quedan dentro de estos semicírculos pero fuera del círculo de diámetro d. ¿Cuál es el área de las dos lúnulas formadas?
Conocimientos necesarios:
Teorema: El ángulo central de un círculo es el doble del ángulo inscrito en él y cuyo arco es el mismo.
Teorema de Pitágoras.
Operaciones con potencias y raíces.
2020-03-17 12:56:25
Arquímedes de Siracusa, propone en el libro de los lemas otro problema interesante.
Sea ABC un semicírculo. Por el punto B se traza una perpendicular BD al diámetro AC y sobre los segmentos AD y DC como diámetros se construyen dos semicírculos AFD y DHC. El área AFDHCB de las dos hoces obtenidas (Arquímedes lo llama arbelon, de árbelos, que es como se llama en griego al cuchillo del zapatero) es igual al área del círculo de diámetro DB. Demuéstralo.
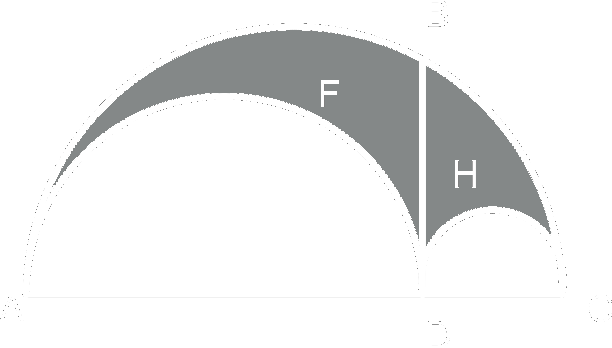
Sólo hace falta recordar el Teorema de Pitágoras y que los segmentos trazados desde cualquier punto de una semicircunferencia hasta los extremos del diámetro forman un ángulo recto (una semicircunferencia es un arco capaz de 90º).
